
闂傚倸鍊搁崐鎼佸磹閹间礁纾归柟闂寸绾惧綊鏌熼梻瀵割槮缁炬儳婀遍埀顒傛嚀鐎氼參宕崇壕瀣ㄤ汗闁圭儤鍨归崐鐐差渻閵堝棗绗傜紒鈧笟鈧畷婊堫敇閻戝棙瀵岄梺闈涚墕濡鎱ㄨ缁辨帡鎮╅崘鑼紝闂佺粯渚楅崳锝嗘叏閳ь剟鏌曢崼婵囶棤闁告ɑ鎹囬弻鈩冨緞鐏炴垝娌繝銏㈡嚀濡繂鐣峰┑鍡╁悑闁糕剝鍔掔花濠氭⒑閸濆嫬鈧悂鎮樺┑瀣垫晜妞ゆ劑鍊楃壕濂稿级閸稑濡界€规洖鐬奸埀顒冾潐濞叉ḿ鏁幒妤嬬稏婵犻潧顑愰弫鍕煢濡警妲峰瑙勬礋濮婃椽宕ㄦ繝鍕窗闂佺ǹ瀛╂繛濠囧箚鐏炶В鏋庨柟鎯ь嚟閸橀亶姊洪崫鍕偍闁告柨鐭傞幃姗€鎮╅悽鐢碉紲闂佺粯鐟㈤崑鎾绘煕閵娿儳鍩g€殿喖顭锋俊鎼佸煛閸屾矮绨介梻浣呵归張顒傜矙閹达富鏁傞柨鐕傛嫹濠电姷鏁告慨鐑藉极閸涘﹥鍙忛柣鎴f閺嬩線鏌涘☉姗堟敾闁告瑥绻橀弻锝夊箣閿濆棭妫勯梺鍝勵儎缁舵岸寮婚悢鍏尖拻閻庨潧澹婂Σ顔剧磼閹冣挃缂侇噮鍨抽幑銏犫槈閵忕姷顓洪梺鍝勫暊閸嬫捇鏌涢妶鍛ч柡灞剧洴婵$兘顢欓悡搴樻嫽闂備浇妗ㄧ粈浣该洪銏犺摕闁哄浄绱曢悿鈧梺鍝勬川閸婎偊濡烽敂杞扮盎闂佹寧妫侀褍鈻嶅澶嬬厵妞ゆ梻鐡斿▓婊呪偓瑙勬礃椤ㄥ棗顕ラ崟顒傜瘈濞达絽澹婂Λ婊堟⒒閸屾艾鈧绮堟笟鈧獮澶愬灳鐡掍焦妞介弫鍐磼濮樻唻绱卞┑鐘灱閸╂牠宕濋弴銏犲強闁靛鏅滈悡鐔兼煙闁箑鏋涢柛鏂款儔閺屽秹鏌ㄧ€n亞浼岄梺璇″枛缂嶅﹪鐛笟鈧獮鎺楀箣濠垫劗鈧櫕绻濋悽闈涗粶闁瑰啿绻樺畷婵嗏枎閹惧疇鎽曢梺缁樻⒒閸樠呯矆閸曨垱鐓忛柛顐g箖椤ユ粍銇勮箛銉﹀



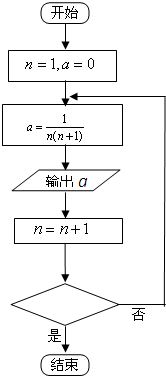 執(zhí)行如圖程序框圖:
執(zhí)行如圖程序框圖: