例1.6本不同的書����,按下列要求各有多少種不同的選法:
(1)分給甲����、乙�����、丙三人����,每人2本�����;
(2)分為三份�,每份2本����;
(3)分為三份���,一份1本��,一份2本���,一份3本;
(4)分給甲�、乙、丙三人�,一人1本,一人2本���,一人3本����;
(5)分給甲、乙���、丙三人�����,每人至少1本
解:(1)根據(jù)分步計數(shù)原理得到: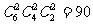 種���;
種���;
(2)分給甲、乙��、丙三人���,每人兩本有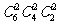 種方法��,這個過程可以分兩步完成:第一步分為三份��,每份兩本�����,設(shè)有x種方法�����;第二步再將這三份分給甲�����、乙����、丙三名同學(xué)有
種方法��,這個過程可以分兩步完成:第一步分為三份��,每份兩本�����,設(shè)有x種方法�����;第二步再將這三份分給甲�����、乙����、丙三名同學(xué)有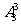 種方法.根據(jù)分步計數(shù)原理可得:
種方法.根據(jù)分步計數(shù)原理可得: ,所以
,所以 .因此����,分為三份�,每份兩本一共有15種方法
.因此����,分為三份�,每份兩本一共有15種方法
點評:本題是分組中的“均勻分組”問題.
一般地:將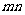 個元素均勻分成
個元素均勻分成 組(每組
組(每組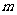 個元素),共有
個元素),共有 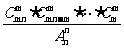 種方法
種方法
(3)這是“不均勻分組”問題����,一共有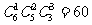 種方法.
種方法.
(4)在(3)的基礎(chǔ)上再進行全排列,所以一共有 種方法.
種方法.
(5)可以分為三類情況:
①“2�����、2����、2型”即(1)中的分配情況�����,有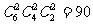 種方法�����;
種方法�����;
②“1��、2��、3型”即(4)中的分配情況����,有 種方法��;
種方法��;
③“1�����、1����、4型”��,有 種方法�,
種方法�,
所以����,一共有90+360+90=540種方法.
例2.身高互不相同的7名運動員站成一排,
(1)其中甲����、乙、丙三人自左向右從高到矮排列的排法有多少種����?
(2)其中甲、乙����、丙三人自左向右從高到矮排列且互不相鄰的排法有多少種�?
解:(1)(法一):設(shè)想有7個位置,先將其他4人排好����,有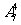 種排法;再將甲���、乙����、丙三人自左向右從高到矮排在剩下的3個位置上,只有1種排法����,根據(jù)分步計數(shù)原理,一共有
種排法;再將甲���、乙����、丙三人自左向右從高到矮排在剩下的3個位置上,只有1種排法����,根據(jù)分步計數(shù)原理,一共有 種方法
種方法
(法二):設(shè)想有7個位置�,先將甲、乙�����、丙三人自左向右從高到矮排在其中的3個位置上�,有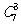 種排法;將其他4人排在剩下的4個位置上��,有
種排法;將其他4人排在剩下的4個位置上��,有 種排法����;根據(jù)分步計數(shù)原理,一共有
種排法����;根據(jù)分步計數(shù)原理,一共有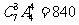 種方法.
種方法.
(2)(插空法)先將其余4個同學(xué)進行全排列一共有 種方法���,再將甲����、乙、丙三名同學(xué)插入5個空位置中(但無需要進行排列)有
種方法���,再將甲����、乙、丙三名同學(xué)插入5個空位置中(但無需要進行排列)有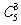 種方法.根據(jù)分步計數(shù)原理����,一共有
種方法.根據(jù)分步計數(shù)原理����,一共有
 種方法.
種方法.
例3.(1) 四個不同的小球放入四個不同的盒中,一共有多少種不同的放法���?
(2) 四個不同的小球放入四個不同的盒中且恰有一個空盒的放法有多少種��?
解:(1)根據(jù)分步計數(shù)原理:一共有 種方法��;
種方法��;
(2)(捆綁法)第一步:從四個不同的小球中任取兩個“捆綁”在一起看成一個元素有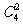 種方法���;第二步:從四個不同的盒中任取三個將球放入有
種方法���;第二步:從四個不同的盒中任取三個將球放入有 種方法,所以�,一共有
種方法,所以�,一共有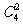
 =144種方法.
=144種方法.
例4.馬路上有編號為1,2�,3��,…�����,10的十盞路燈,為節(jié)約用電又不影響照明�,可以把其中3盞燈關(guān)掉,但不可以同時關(guān)掉相鄰的兩盞或三盞���,在兩端的燈都不能關(guān)掉的情況下�,有多少種不同的關(guān)燈方法����?
解:(插空法)本題等價于在7只亮著的路燈之間的6個空檔中插入3只熄掉的燈,故所求方法總數(shù)為 種方法
種方法
例5.九張卡片分別寫著數(shù)字0��,1����,2,…�����,8�,從中取出三張排成一排組成一個三位數(shù),如果6可以當作9使用�,問可以組成多少個三位數(shù)?
解:可以分為兩類情況:① 若取出6,則有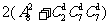 種方法�;
種方法�;
②若不取6,則有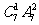 種方法�����,
種方法�����,
根據(jù)分類計數(shù)原理��,一共有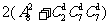 +
+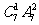 =602種方法
=602種方法 