闂傚倸鍊搁崐鎼佸磹閹间礁纾归柟闂寸绾惧綊鏌熼梻瀵割槮缁炬儳缍婇弻鐔兼⒒鐎靛壊妲紒鐐劤缂嶅﹪寮婚悢鍏尖拻閻庨潧澹婂Σ顔剧磼閻愵剙鍔ゆ繝鈧柆宥呯劦妞ゆ帒鍊归崵鈧柣搴㈠嚬閸欏啫鐣峰畷鍥ь棜閻庯絻鍔嬪Ч妤呮⒑閸︻厼鍔嬮柛銊ョ秺瀹曟劙鎮欏顔藉瘜闂侀潧鐗嗗Λ妤冪箔閸屾粎纾奸柍褜鍓氱粭鐔煎焵椤掆偓閻e嘲饪伴崼顐f櫍闂佺粯鍨靛Λ娆戔偓闈涚焸濮婃椽妫冨☉姘暫濠碘槅鍋呴〃鍡涘箞閵婎煈妲剧紓浣介哺鐢繝骞冮埡鍛闁肩⒈鍏涚槐婵嬫⒒娴h櫣甯涘〒姘殜瀹曟娊鏁愰崱妯哄伎闂侀€炲苯澧撮柡灞炬礋瀹曠厧鈹戦崶鑸碉骏闂備礁鎲¤摫闁圭懓娲濠氬焺閸愩劎绐為柣蹇曞仦閸ㄦ繂鈻介鍛瘈闁靛繈鍨洪崵鈧┑鈽嗗亝缁诲倿鎮惧畡鎵虫斀闁糕檧鏅涢幃鎴︽⒑缁洖澧查柛鏃€甯為懞杈ㄧ節濮橆厸鎷洪梺鍛婄箓鐎氼剟鍩€椤掍焦鍊愰柟顔矫埞鎴犫偓锝呯仛閺呮粌顪冮妶鍡楀闁稿﹥顨堟竟鏇熺附缁嬭法楠囬梺鍓插亝缁嬫垶淇婇悾灞稿亾鐟欏嫭绀€闁活剙銈搁崺鈧い鎺戝枤濞兼劖绻涢崣澶呯細闁轰緡鍣i獮鎺懳旂€n剛鈼ゆ繝鐢靛█濞佳囶敄閹版澘鏋侀柛鏇ㄥ灡閻撱垺淇婇娆掝劅婵℃彃鍢查…璺ㄦ喆閸曨剛顦板┑顔硷攻濡炶棄鐣烽妸锔剧瘈闁告洦鍘剧粣妤呮⒒娴e懙鍦偓娑掓櫆缁绘稒绻濋崶褏鐣鹃柣蹇曞仩琚欓柡瀣叄閺岀喖骞嗚閸ょ喖鏌涘鈧禍璺侯潖濞差亜浼犻柛鏇ㄥ墮閸嬪秹姊洪崨濠冪叆闁活厼鍊块獮鍐潨閳ь剟骞冮埡鍛仺闁汇垻顣槐鏌ユ⒒娴h櫣甯涢柣鐔村灲瀹曟垿骞樼紒妯煎幈闂侀潧枪閸庢娊宕洪敐鍥e亾濞堝灝鏋涙い顓㈡敱娣囧﹪骞栨担鍝ュ幐闂佺ǹ鏈惌顔捐姳娴犲鈷掑ù锝呮嚈瑜版帒瀚夋い鎺戝€婚惌娆撴煙鏉堟儳鐦滈柡浣稿€块弻銊╂偆閸屾稑顏�濠电姷鏁告慨鐑藉极閸涘﹥鍙忛柣鎴f閺嬩線鏌涘☉姗堟敾闁告瑥绻橀弻锝夊箣閿濆棭妫勯梺鍝勵儎缁舵岸寮诲☉妯锋婵鐗婇弫楣冩⒑閸涘﹦鎳冪紒缁橈耿瀵鏁愭径濠勵吅闂佹寧绻傚Λ顓炍涢崟顖涒拺闁告繂瀚烽崕搴g磼閼搁潧鍝虹€殿喖顭烽幃銏ゅ礂鐏忔牗瀚介梺璇查叄濞佳勭珶婵犲伣锝夘敊閸撗咃紲闂佽鍨庨崘锝嗗瘱缂傚倷绶¢崳顕€宕归幎钘夌闁靛繒濮Σ鍫ユ煏韫囨洖啸妞ゆ挻妞藉娲传閸曨偅娈滈梺绋款儐閹瑰洭寮诲☉銏犖ч柛娑卞瀺瑜旈弻锛勪沪閸撗勫垱婵犵绱曢崗姗€銆佸▎鎾村亗閹煎瓨蓱鐎氫粙姊婚崒娆愮グ婵℃ぜ鍔庣划鍫熸媴鐠囥儲妞介、姗€濮€閻樼儤鎲伴梻浣告惈濞村嫮妲愰弴銏″仾闁逞屽墴濮婃椽宕崟顒€绐涢梺绋库看閸嬪﹥淇婇悜鑺ユ櫆閺夌偞澹嗛惄搴ㄦ⒒娴g懓顕滄俊顐$窔椤㈡俺顦查柍璇茬Т椤撳吋寰勭€n剙骞嶆俊鐐€栧濠氭偤閺傚簱鏋旀繝濠傛噳閸嬫挾鎲撮崟顒傤槰濡炪們鍔屽Λ妤咁敋閵夆晛绀嬫い鎺戝€婚惁鍫熺箾鏉堝墽鍒板鐟帮工铻炴繝濠傜墛閳锋帡鏌涚仦鎹愬闁逞屽墴椤ユ挾鍒掗崼鐔虹懝闁逞屽墴閻涱喗寰勯幇顒備紜闁烩剝甯婇悞锕€顪冩禒瀣瀬闁告劦鍠栫壕鍏兼叏濡鏁剧紒鍗炲船閳规垿鎮╅鑲╀紘闂佺硶鏅滈悧鐘茬暦濠靛鍗抽柕蹇曞Т瀵兘姊洪棃娑辨Т闁哄懏绮撻幃锟犳偄閸忚偐鍘甸梻渚囧弿缁犳垿寮稿☉銏$厱闁哄倹顑欓崕鏃堟煛鐏炵晫效闁哄被鍔庨埀顒婄秵娴滅偞瀵煎畝鍕拺閻犲洠鈧櫕鐏堢紓鍌氱Т閿曨亪鎮伴鐣岀懝闁逞屽墴閻涱噣骞掑Δ鈧粻锝嗙節閸偄濮夐柍褜鍓濆▍鏇犳崲濠靛鍋ㄩ梻鍫熺◥缁爼姊洪悷鏉挎毐缂佺粯锚閻e嘲鈹戦崱蹇旂€婚梺瑙勫劤閻ゅ洭骞楅弴銏♀拺缂備焦蓱閳锋帡鏌涘Ο鐘叉噽閻棝鏌涢弴銊ョ仭闁绘挸绻橀弻娑㈩敃閿濆洨鐣哄銈冨劜缁秹濡甸崟顔剧杸闁靛绠戦锟�
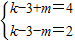 或
或