
題目列表(包括答案和解析)
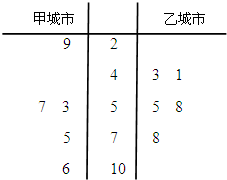 (2013•朝陽區(qū)一模)國家環(huán)境標準制定的空氣質(zhì)量指數(shù)與空氣質(zhì)量等級對應(yīng)關(guān)系如下表:
(2013•朝陽區(qū)一模)國家環(huán)境標準制定的空氣質(zhì)量指數(shù)與空氣質(zhì)量等級對應(yīng)關(guān)系如下表:| 空氣質(zhì)量指數(shù) | 0-50 | 51-100 | 101-150 | 151-200 | 201-300 | 300以上 |
| 空氣質(zhì)量等級 | 1級優(yōu) | 2級良 | 3級輕度污染 | 4級中度污染 | 5級重度污染 | 6級嚴重污染 |
| 1 |
| n |
. |
| x |
. |
| x |
. |
| x |
. |
| x |
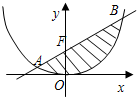 如圖,設(shè)由拋物線C:x2=4y與過它的焦點F的直線l所圍成封閉曲面圖形的面積為S(陰影部分).
如圖,設(shè)由拋物線C:x2=4y與過它的焦點F的直線l所圍成封閉曲面圖形的面積為S(陰影部分).| x |
| 2 |
| sinx |
| 4 |
| 2x+15 |
| 18 |
| x2+15 |
| 18 |
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com