
ҝЖДҝЈә ҒнФҙЈә о}РНЈә
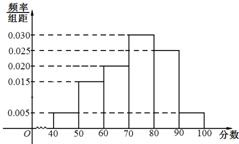 ДіРЈҸД…ўјУёЯ¶юДкјүҢWҳI(yЁЁ)Л®ЖҪңyФҮөДҢWЙъЦРійіц80ГыҢWЙъЈ¬Жд”ө(shЁҙ)ҢWіЙҝғЈЁҫщһйХы”ө(shЁҙ)Ј©өДоlВК·ЦІјЦұ·ҪҲDИзҲDЛщКҫЈ®
ДіРЈҸД…ўјУёЯ¶юДкјүҢWҳI(yЁЁ)Л®ЖҪңyФҮөДҢWЙъЦРійіц80ГыҢWЙъЈ¬Жд”ө(shЁҙ)ҢWіЙҝғЈЁҫщһйХы”ө(shЁҙ)Ј©өДоlВК·ЦІјЦұ·ҪҲDИзҲDЛщКҫЈ®Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈә ҒнФҙЈә о}РНЈә

Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈә ҒнФҙЈә о}РНЈә
| јЧ | ТТ | ||||||||||||||||||
| ӯh(huЁўn)”ө(shЁҙ) | 8 | 9 | 10 | ӯh(huЁўn)”ө(shЁҙ) | 8 | 9 | 10 | ||||||||||||
| ёЕВК |
|
|
|
ёЕВК |
|
|
| ||||||||||||
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈә ҒнФҙЈә о}РНЈә
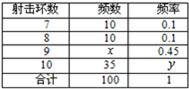
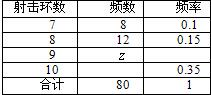
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈә ҒнФҙЈә о}РНЈә
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈә ҒнФҙЈә о}РНЈә
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈә ҒнФҙЈә о}РНЈә
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈә ҒнФҙЈә о}РНЈә
| 1 |
| 3 |
| 16 |
| 3 |
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈә ҒнФҙЈә о}РНЈә
| y2 |
| 4 |
| ҰР |
| 4 |
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈә ҒнФҙЈә о}РНЈә
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 4 |
|
Ійҝҙҙр°ёәНҪвОц>>
°Щ¶ИЦВРЕ - ҫҡБ•ғФБРұн - ФҮо}БРұн
әюұұКЎ»ҘВ“(liЁўn)ҫW(wЁЈng)Я`·ЁәНІ»БјРЕПўЕeҲуЖҪЕ_ | ҫW(wЁЈng)ЙПУРәҰРЕПўЕeҲуҢЈ…^(qЁұ) | лҠРЕФpт_ЕeҲуҢЈ…^(qЁұ) | ЙжҡvК·М“ҹoЦчБxУРәҰРЕПўЕeҲуҢЈ…^(qЁұ) | ЙжЖуЗЦҷа(quЁўn)ЕeҲуҢЈ…^(qЁұ)
Я`·ЁәНІ»БјРЕПўЕeҲулҠФ’Јә027-86699610 ЕeҲуа]ПдЈә58377363@163.com